Anzahl der Prüflinge

 

Die Anzahl der Prüflinge, die getestet werden müssen, um die Randbedingungen zu erfüllen, kann abhängig von den bekannten Vorgaben berechnet werden.

Die Unterpunkte berücksichtigen die unterschiedlichen Vorgaben sowie die Verteilung, die bei der Berechnung des Ergebnisses angenommen wurde.

 

Nach Weibull

 

Bei der Berechnung nach Weibull wird auf Basis einer Weibull-Verteilung bei vorgegebener Aussagewahrscheinlichkeit, Mindestzuverlässigkeit und der Ranggröße i die Mindestanzahl der Prüflinge berechnet.

 

Verteilung:                        Weibull

Vorgaben (müssen eingegeben werden):

                                      Aussagewahrscheinlichkeit             P_A

                                      Mindestzuverlässigkeit                   R

                                      Ranggröße                                  i

 

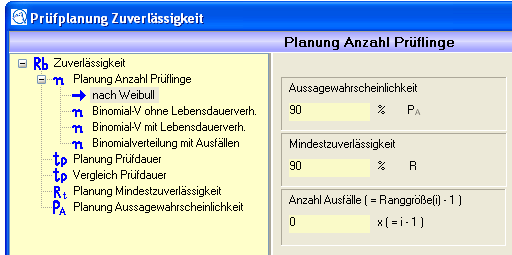
Abbildung 2: Weibull Eingabe

 

Nach Klick auf den OK-Button oder in den grünen Bereich unter den Eingabefeldern berechnet das Programm die Mindestanzahl der zu prüfenden Teile.

 

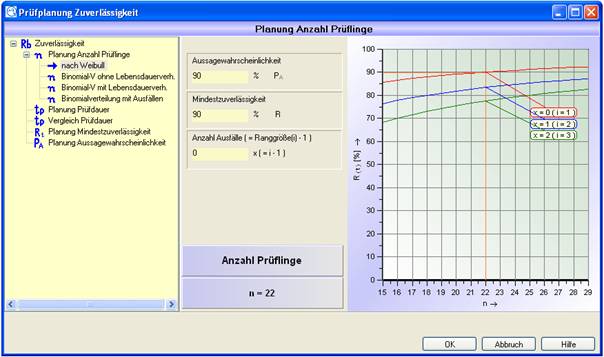
Abbildung 3: Weibull Ergebnis

 

Als Grafik werden zu der durch die Eingaben vorgegebenen Kurve für die Mindestzuverlässigkeit noch 2 weitere Kurven für unterschiedliche Ranggrößen i dargestellt.

Die Ergebniskurve erkennt man an dem Schnittpunkt von berechnetem n und vorgegebener Mindestzuverlässigkeit (im Beispiel n = 38, R_(t) = 90).

Die Farben der Kurven lassen sich standardmäßig über die Einstellungen definieren. Hierbei ist die Kurve des Ergebnisses immer die 2. Auswahlmöglichkeit.

 

 

Beispiel 1:

Für ein Fahrzeuggetriebe wird im Lastenheft die Lebensdauer B₁₀ = 250000 km mit einer Aussagewahrscheinlichkeit von P_A = 95% gefordert.

Ermittelt werden soll die erforderliche Getriebeanzahl für die Prüfung ohne Ausfall.

(vgl. VDA 3 S. 72 Beispiel 2.7 a))

 

 

Lösung:

 

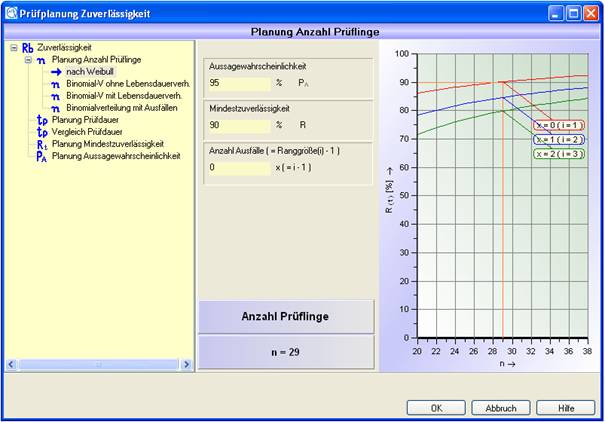
Abbildung 4: Lösung Beispiel 1

 

 

Binomial ohne Lebensdauerverhältnis

 

Verteilung:                        Binomialverteilung

Vorgaben (müssen eingegeben werden):

                                      Aussagewahrscheinlichkeit             P_A

                                      Mindestzuverlässigkeit                   R

 

 

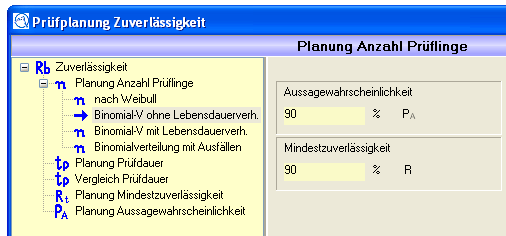
Abbildung 5: Eingabe Binomial ohne Lebensdauerverhältnis

 

Als Ergebnis werden Kurven mit unterschiedlichen Aussagewahrscheinlichkeiten angezeigt.

 

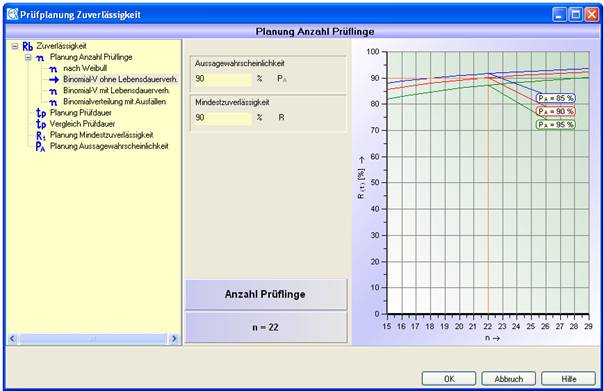
Abbildung 6: Ergebnis Binomial ohne Lebensdauerverhältnis

 

Beispiel 2:

Für ein Fahrzeuggetriebe wird im Lastenheft die Lebensdauer B₁₀ = 250000 km mit einer Aussagewahrscheinlichkeit von P_A = 95% gefordert.

Ermittelt werden soll die erforderliche Getriebeanzahl für die Prüfung ohne Ausfall.

(vgl. VDA 3 S. 72 Beispiel 2.7 b))

 

Lösung:

 

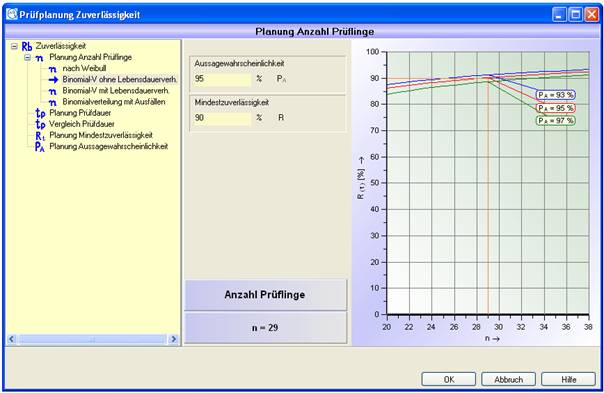
Abbildung 7: Lösung Beispiel 2

 

 

 

Binomial mit Lebensdauerverhältnis

 

Verteilung:                        Binomialverteilung

Vorgaben (müssen eingegeben werden):

                                      Aussagewahrscheinlichkeit             P_A

                                      Mindestzuverlässigkeit                            R

                                      Ausfallsteilheit                                       b

                                      Lebensdauerverhältnis                   L_V

                                                         

                                                L_V := Prüfdauer/Lebensdauer = t_p/t

                                      bzw. Prüfdauer                                      t_P

                                      und Lebensdauer                          t

                                                         

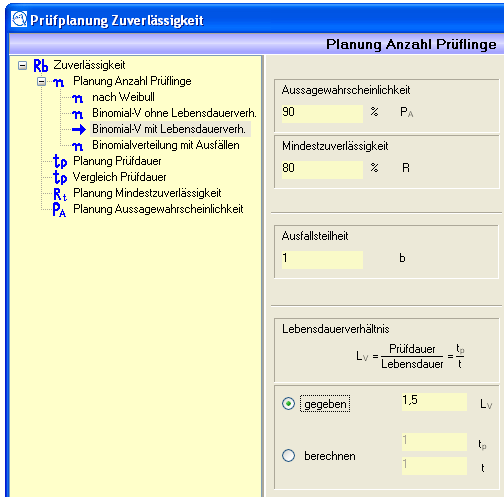
Abbildung 8: Eingabe Binomial mit Lebensdauerverhältnis

 

Das Lebensdauerverhältnis kann wahlweise vorgeben (Radiobutton „gegeben“) oder berechnet (Radiobutton „berechnen“) werden. Soll das Lebensdauerverhältnis berechnet werden, müssen die Prüf- und Lebensdauer vorgegeben werden.

 

In der Grafik zu dem ermittelten Ergebnis für die Anzahl der Prüflinge werden 2 weitere Kurven angezeigt, bei denen die Ausfallsteilheit b variiert wird.

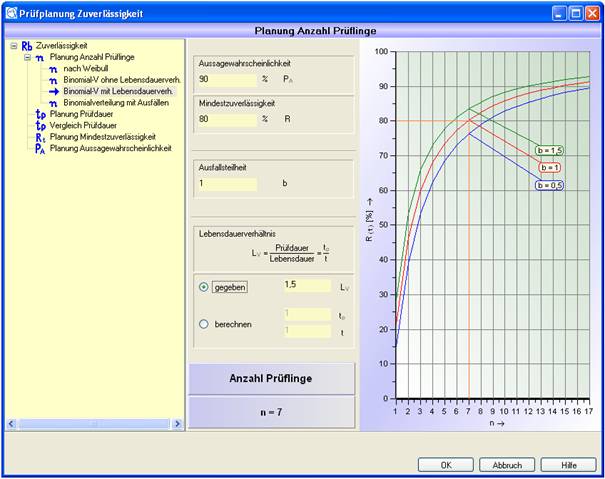
Abbildung 9: Ergebnis Binomial mit Lebensdauerverhältnis

 

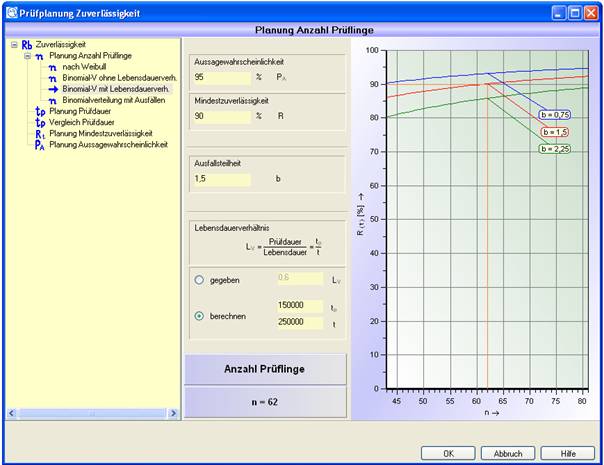
Beispiel 3:

Für ein Fahrzeuggetriebe wird im Lastenheft die Lebensdauer B₁₀ = 250000 km mit einer Aussagewahrscheinlichkeit von P_A = 95% gefordert.

Ermittelt werden soll die erforderliche Getriebeanzahl für die Prüfung ohne Ausfall.

Aus zeitlichen Gründen steht nur die Zeit für 150000 Versuchskilometer je Getriebe zur Verfügung. Wie viele Getriebe müssen geprüft werden?

(vgl. VDA 3 S. 72 Beispiel 2.7 c))

 

Lösung:

 

         

 

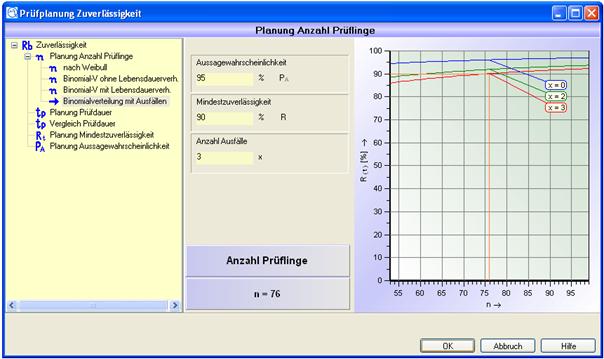
Binomial mit Ausfällen

 

Treten während des Tests Ausfälle auf, gilt für die Aussagewahrscheinlichkeit der Binomialsatz:

 

 

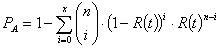
Dabei bezeichnet x die Anzahl der Ausfälle im Zeitraum t und n ist der Stichprobenumfang.

 

Verteilung:                        Binomialverteilung

Vorgaben (müssen eingegeben werden):

 

Abbildung 10: Lösung Beispiel 3

	Aussagewahrscheinlichkeit	PA
	Mindestzuverlässigkeit	R
	Anzahl der Ausfälle	x

 

 

 

 

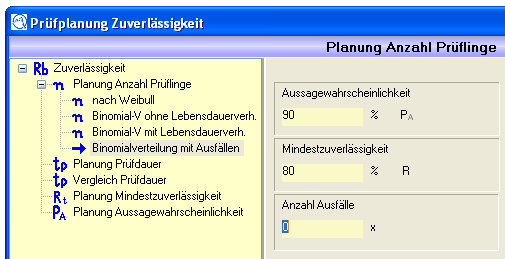
Abbildung 11: Eingabe Binomial mit Ausfällen

 

In der Darstellung des Ergebnisses wird für die beiden zusätzlichen Kurven die Anzahl der maximalen Ausfälle verändert.

 

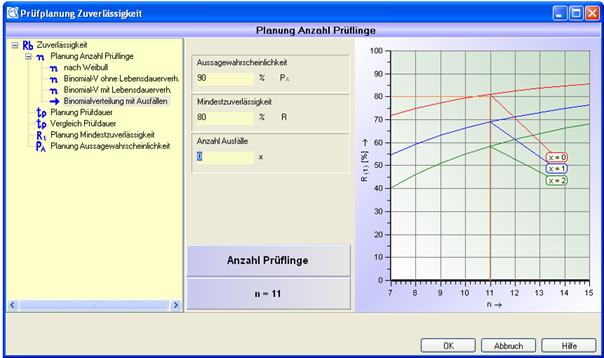
Abbildung 12: Ergebnis Binomial mit Ausfällen

 

Beispiel 4:

Die Lebensdauerversuche wurden mit der Stichprobenanzahl gemäß Beispiel 12 durchgeführt. Drei Getriebe sind jedoch vor 250000 km Laufleistung ausgefallen, d.h. x=3. Die anderen n – x Getriebe haben die geforderte B₁₀-Laufleistung ohne Ausfall überlebt.

Wie viele Getriebe n* müssten wegen der aufgetretenen Ausfälle zusätzlich bis zur B10-Lebensdauer ohne Ausfall geprüft werden, um die geforderte Zuverlässigkeit mit der geforderten Aussagewahrscheinlichkeit nachzuweisen?

(vgl. VDA 3 S. 72 Beispiel 2.7 g))

 

Lösung: