Testverfahren
Mit Hilfe numerischer Testverfahren sollen Informationen über signifikante Eigenschaften einer Messwertreihe gewonnen werden. Die Vorgehensweise lässt sich wie folgt zusammenfassen:
1. Aufstellen der Nullhypothese H0
2. Aufstellen der Alternativhypothese H1
3. testspezifische Berechnung der jeweiligen Prüfgröße
4. Vergleich der Prüfgröße mit den testspezifischen
kritischen Werten für die Signifikanzniveaus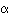 
= 0,1%, 1%, 5%
5. Testergebnis: Unter- bzw. überschreitet die Prüfgröße einen der kritischen Werte, wird die Nullhypothese zugunsten der Alternativhypothese verworfen
Um sich schnell einen Überblick zu verschaffen, ist die Anwendung mehrerer Testverfahren notwendig. Einer übersichtlichen Darstellung der Ergebnisse kommt damit ein hoher Stellenwert zu. Unterschieden wird zwischen der Darstellung einzelner Testergebnisse und einer Übersicht über mehrere Ergebnisse.
Interpretation der Darstellung
Ist die errechnete Prüfgröße mit keinem Stern gekennzeichnet, so kann von der Nullhypothese ausgegangen werden. Das Feld ist dann grün unterlegt. Ist die Prüfgröße mit einem oder mehreren Sternen versehen, so ist bei:
• * mit einer Wahrscheinlichkeit von 95% (gelb)
• ** mit einer Wahrscheinlichkeit von 99% (rot)
• *** mit einer Wahrscheinlichkeit von 99,9% (rot)
die Alternativhypothese zutreffend.
Fehlen die kritischen Werte, so sind diese nicht bekannt und können daher nicht berücksichtigt werden. Das kann dazu führen, dass ein Testverfahren nicht durchführbar ist. Es erscheint dann die Fehlermeldung: "Test konnte bei dem vorliegenden Verteilungsmodell nicht durchgeführt werden". Sind bestimmte Voraussetzungen nicht erfüllt, erscheint ebenfalls eine Fehlermeldung mit entsprechender Erläuterung.
Übersicht