Testverfahren

 

 

Die Darstellung der Einzelergebnisse enthält die Aussagen der Null- und Alternativhypothese, die kritischen Werte für die jeweiligen Signifikanzniveaus, die berechnete Prüfgröße sowie das Testergebnis. In der Kopfzeile sind Testverfahren und Teile- und Merkmalsnummer der ausgewerteten Messwertreihe eingeblendet.

 

Folgende Testverfahren stehen zur Auswahl bzw. können angezeigt werden:

Tests auf Zufälligkeit

Für eine Aussage über einen bestimmten Sachverhalt in der Grundgesamtheit muss u.a. gewährleistet sein, dass die Ergebnisse der Untersuchung unabhängig vom Umfang der Stichprobe sind. Das setzt i.a. eine zufällige Anordnung des Datenmaterials voraus. Durch einen Test auf Zufälligkeit können nicht zufällige Wertefolgen von Einzel- und Mittelwerten erkannt werden.

Test nach Swed und Eisenhart

Dieser Test beruht auf der Analyse des Verlaufs der Werte im Vergleich zum Medianwert. Hierbei werden sogenannte Runs gebildet (Folge von Werten, die ausschließlich unterhalb bzw. oberhalb des Medians liegen). Die Gesamtzahl der Runs dient als Prüfgröße, die mit dem testspezifischen kritischen Wert verglichen wird. Damit ist eine Aussage möglich, ob die Anordnung der Werte zufällig ist oder nicht.

 

Test auf Trend

Test auf sukzessive Differenzstreuung

Dieser Trendtest anhand der Streuung zeitlich aufeinanderfolgender Stichprobenwerte basiert auf dem Verhältnis der sukzessiven Differenzstreuung zur Varianz. Unterschreitet diese Prüfgröße den testspezifischen kritischen Wert liegt ein Trend vor, da dann benachbarte Werte ähnlicher sind als entferntere.

 

Tests auf Normalverteilung

Bei einigen statistischen Verfahren, insbesondere bei der Stichprobenprüfung anhand quantitativer Merkmale, sind die Aussagen nur dann zutreffend, wenn die Werte aus einer normalverteilten Grundgesamtheit stammen. Das Testen der Normalverteilung unter Ausnutzung aller zur Verfügung stehenden Informationen ist daher unumgänglich.

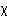²-Test

Bei diesem Test wird die Stichprobe klassiert und aus der angenommenen Verteilungsfunktion (hier Normalverteilung) die theoretisch zu den Klassen gehörenden Wahrscheinlichkeiten berechnet. Diese Erwartungswerte werden mit den Klassenhäufigkeiten der gegebenen Stichprobe, den Beobachtungswerten, verglichen.

Anmerkung: Bei zu geringer Klassenanzahl bzw. zu geringen Besetzungszahlen kann der 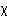²-Test nicht durchgeführt werden.

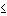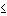D' Agostino Test (50  n  1000)

Bei diesem Test handelt es sich nicht um einen gezielten Anpassungstest auf Normalverteilung. Er ist daher in der neuen ISO/DIS 5479 (Tests auf Normalverteilung) nicht mehr enthalten. Der Vollständigkeit halber ist dieser Test aber in qs-STAT noch verfügbar.

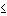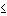Epps-Pulley-Test (8  n  200)

Dieser Test ist als Ersatz für den d`Agostino-Test in der Norm ISO/DIS 5479 enthalten.

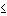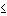Shapiro-Wilk-Test (3  n  50)

Der Shapiro-Wilk-Test ist ein weiteres Verfahren, um festzustellen, ob die Stichprobe aus einer normalverteilten Grundgesamtheit stammt.

Erweiterter Shapiro-Wilk-Test (kleine Stichprobengrößen)

Dieses Testverfahren dient zur gemeinsamen Beurteilung mehrerer Stichprobenergebnisse. Es bietet sich beim Vorliegen von Stichproben mit wenigen Werten an, da hier eine separate Beurteilung der Normalität mit einer großen Unsicherheit verbunden wäre. Da das Testverfahren nur bei der Beurteilung von mehreren Stichproben verwendet wird, steht es nur im Modul Prozessanalyse zur Verfügung.

Neben dem numerischen Testergebnis lässt sich die Normalität auch grafisch prüfen. Beim erweiterten Shapiro-Wilk-Test wird für jede Stichprobe eine Kenngröße berechnet und diese in ein W-Netz eingetragen. Liegen nun der Mittelwert der Kenngrößen bei 0 und die Standardabweichung bei 1, kann von einer normalverteilten Grundgesamtheit ausgegangen werden. Die Darstellung im W-Netz ist über den Menüpunkt "Kennwerte" - "Wahrscheinlichkeitsnetz" - "erweiterter Shapiro-Wilk-Test" aufrufbar.

Asymmetrie-Test

Dieser Test beschreibt die Schiefe (links- bzw. rechtssteil) einer Verteilung. Die Prüfgröße ist mit dem statistischen Kennwert "Schiefe" identisch.

Kurtosis-Test

Dieser Test beschreibt die Wölbung (steil- oder flachgipflig) einer Verteilung. Die Prüfgröße ist mit dem statistischen Kennwert "Wölbung" identisch.

 

Vergleich von Varianzen und Mittelwerten

t-Test (Vergleich der Mittelwerte von zwei Grundgesamtheiten)

Aufgrund zweier Stichprobenmittelwerte soll geprüft werden, ob sich die Mittelwerte der beiden Grundgesamtheiten wesentlich unterscheiden.

Mit dem t-Test, hier der zweiseitige, wird die Nullhypothese H0 gegen die Alternativhypothese H1 geprüft.

Nullhypothese H0 : µ1 = µ2 Die beiden Stichproben entstammen Grundgesamtheiten, deren Mittelwerte einander gleich sind.

Alternativhypothese H1 : µ1 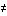 µ2 Die beiden Stichproben entstammen Grundgesamtheiten, deren Mittelwerte nicht gleich sind.

F-Test (Vergleich der Varianzen von zwei Grundgesamtheiten)

Basierend auf den Varianzen zweier Stichproben überprüft der F-Test, ob sich die Varianzen der beiden Grundgesamtheiten wesentlich voneinander unterscheiden.

Varianzanalyse nach dem ANOVA-Modell (F-Test)

Bei diesem Test wird geprüft, ob zwischen der inneren (innerhalb der Stichproben) und der äußeren Streuung (zwischen den Stichproben) signifikante Abweichungen bestehen.