Assistent (Planen / Durchführen): Auswahl

Trotz aller Bemühungen lassen sich Fehler in der Beschreibung nie vollständig vermeiden. Für Ihre Hinweise und Anregungen sind wir jederzeit dankbar (Hotline: hotline@q-das.de, +49 (6201) 3941-14).

Allgemein

Dies ist die Einstiegsmaske für die Durchführung der Tests. Auf der linken Seite finden sie die Möglichkeit Einstellungen vorzunehmen , die Hilfe aufzurufen , die laufende Berechnung abzubrechen , oder nach der Auswahl eines Test weiter zu gehen .

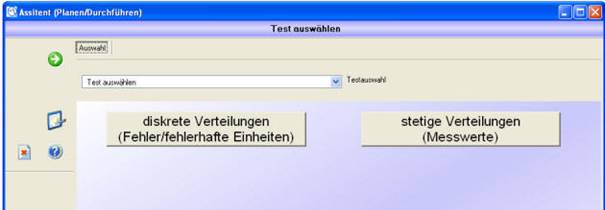
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\Testverfahren_Auswahl-Dateien\Testve1.JPG$

Testauswahl

Die Auswahl des durchzuführenden Tests erfolgt entweder durch Zuweisen eines Tests über die Auswahlbox „Testauswahl“ oder durch Anklicken eines Testes in dem Entscheidungsbaum.

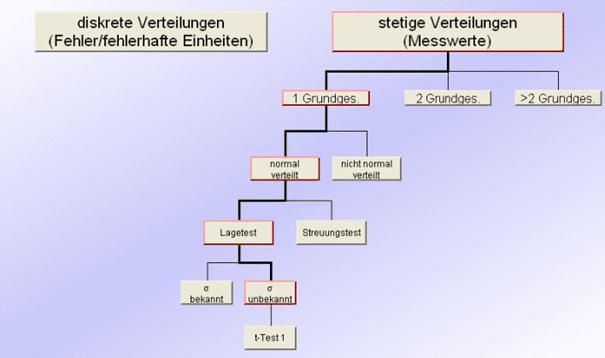
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\Testve3.GIF$

Durch die schrittweise Entscheidungsfindung im Ablaufbaum gelangt der Anwender zu einem durchzuführenden Test. Dabei werden die alternativen Möglichkeiten auf jeder Entscheidungsebene angezeigt. So sollte der zur Aufgabenstellung passende Test schnell gefunden werden.

Nachdem ein Test festgelegt wurde, kann in die Testdurchführung bzw. Testplanung gewechselt werden (Buttons oder Register werden aktiv).

Theorie der Tests

Allgemeine Denkweise bei Testverfahren
Ein Betrieb regelt die Qualität seiner Erzeugnisse, indem er alle 30 Minuten eine Stichprobe entnimmt. Die Merkmale, auf die es ankommt (z.B. Länge, Durchmesser, Festigkeit etc.) wurden gemessen und die Kenngrößen ermittelt. Diese Kenngrößen unterliegen jedoch kleinen zufälligen Schwankungen, hervorgerufen durch Unregelmäßigkeiten des Materials, der Maschinen, auf denen gefertigt wird, und dem Bedienpersonal.

Nimmt man an, die Länge der gefertigten Teile soll 20 mm betragen, so lautet die Hypothese µ = 20 mm. Weicht nun der Mittelwert 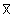$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\Testverfahren_Auswahl-Dateien\image048.gif$ der Stichprobe nicht "zu stark" von µ = 20 mm ab, so nimmt man die Hypothese an und lässt die Produktion weiterlaufen. Ist die Abweichung jedoch "zu groß", so verwirft man die Hypothese, stoppt die Produktion und sucht nach der Ursache der Abweichung.

Wo liegt jedoch die Grenze zwischen kleinen, rein zufälligen Abweichungen und größeren Abweichungen, die nicht mehr alleine durch den Zufall erklärbar sind? Letztere werden als signifikante Abweichungen bezeichnet. Um hierüber objektive Aussagen zu bekommen wurden numerische Testverfahren entwickelt. Alle Verfahren haben folgende Denkweise gemeinsam.

Bei Testverfahren kennt man die hypothetischen Annahmen:

• H₀: Nullhypothese

• H₁: Alternativhypothese.

Für einen Test auf Normalverteilung, bedeutet das Zutreffen der Nullhypothese, dass die Werte aus einer normalverteilten Grundgesamtheit stammen und das Zutreffen von H₁, dass die Grundgesamtheit nicht normalverteilt ist. Damit ergeben sich beim Testen folgende vier Möglichkeiten beim Gegenüberstellen der Wirklichkeit mit der getroffenen Entscheidung:

		WIRKLICHKEIT
		H₀ trifft zu	H₁ trifft zu
Testergebnis	H₀	richtige Entscheidung !	falsche Entscheidung! Wahrscheinlichkeit für diesen Fehler 2. Art ist b
	H₁	falsche Entscheidung! Wahrscheinlichkeit für diesen Fehler 1. Art ist a	richtige Entscheidung !

Von einem Fehler im Ansatz spricht man dann, wenn die dem statistischen Verfahren zu Grunde liegenden Annahmen und/oder Voraussetzungen in Wirklichkeit nicht zutreffen.

Da beim Testen von Hypothesen der wahre Sachverhalt nicht bekannt ist, gibt es keine vollkommen sicheren Schlüsse. Jede Entscheidung ist daher mit einem Fehlerrisiko behaftet.

Aus der Annahme der Nullhypothese aufgrund des Testergebnisses folgt noch nicht, dass die Nullhypothese unbedingt zutreffend sein muss. Wählt man das Signifikanzniveau niedrig, so verringert sich nur das Risiko, einen Fehler 1. Art (Wahrscheinlichkeit a) zu begehen, während bei gleichen Prüfbedingungen das Risiko für einen Fehler 2. Art (Wahrscheinlichkeit ß) steigt. Man sollte bestrebt sein, die Fehlerwahrscheinlichkeit für Fehler beider Arten möglichst klein zu wählen. Bei vielen Tests gibt man sich jedoch oft nur das Signifikanzniveau a vor, ohne eine Aussage über die Größe des Fehlers 2. Art zu machen. In solchen Fällen sollte man auch nicht davon sprechen, dass die Nullhypothese angenommen wurde, sondern davon, dass sie "nicht verworfen" bzw. "nicht widerlegt" werden konnte.

Stellt sich heraus, dass die Wahrscheinlichkeit für den Fehler 2. Art zu groß ist, so kann man sich helfen, indem man den Test mit einer größeren Stichprobe wiederholt.

Woher stammen die Hypothesen?

• Aus Forderungen, die erfüllt werden müssen

• Man kennt den interessierenden Wert aus langer Erfahrung

• Aus einer Theorie, die man überprüfen möchte

• Reine Vermutungen, durch Wünsche oder Beobachtungen angeregt.

Im technischen Bereich ist folgende Vorgehensweise üblich:

Es werden drei verschiedene Signifikanzniveaus festgesetzt. Die Schwellenwerte des größeren Signifikanzniveaus dienen als Kriterium zum "nicht Verwerfen" der Nullhypothese, die Schwellenwerte des kleineren zum "Verwerfen" der Nullhypothese. Es verringern sich durch diese Vorgehensweise sowohl die Fehler erster, als auch die Fehler zweiter Art. Man erhält jedoch eine indifferente Zone, in der keine Entscheidung über das Testergebnis getroffen werden kann. Liegt die Prüfgröße in dieser Zone, so kann eine Wiederholung der Tests mit einer größeren Stichprobe erst eine eindeutige Entscheidung ermöglichen.

Eine in der angewandten Statistik gebräuchliche Darstellungsweise von Testergebnissen sieht folgendermaßen aus:

xxxxx - Name des Tests - xxxxx
Nullhypothese : < Aussage >
Alternativhypothese : < Aussage >
Signifikanz-	kritische Werte		Prüfgröße
niveaus	unten	oben
a = 5 % :	xxxxx	xxxxx
a = 1 % :	xxxxx	xxxxx	xxxxx < ,,** >
a = 0,1 % :	xxxxx	xxxxx

Interpretation der Darstellung

Ist die errechnete Prüfgröße, die mit den kritischen Werten aus einer Tabelle verglichen werden, mit keinem Stern gekennzeichnet, so kann von der Nullhypothese ausgegangen werden.

Ist die Prüfgröße mit einem oder mehreren Sternen versehen, so ist bei:

* mit einer Wahrscheinlichkeit von 95%

** mit einer Wahrscheinlichkeit von 99%

*** mit einer Wahrscheinlichkeit von 99,9%

die Alternativhypothese zutreffend.

Mehr:

Einstellung Testverfahren

Assistent (Planen / Durchführen): Daten

Assistent (Planen / Durchführen): Planung

Assistent (Planen / Durchführen): Testen