QRK für attributive Merkmale

Je nachdem wo dieser Dialog aufgerufen wurde wird dieser entweder mit oder ohne Vorschau dargestellt.

Die Qualitätsregelkarten für attributive Merkmale basieren auf dem Vorhandensein und Entdecken von fehlerhaften Einheiten. Damit warnen sie erst vor negativen Prozessänderungen, wenn bereits eine Anzahl Fehler aufgetreten ist.

Die Bestimmung der Eingriffsgrenzen basiert bei attributiven Merkmalen entweder auf dem Zufallsstreubereich der Binomialverteilung (Anzahl/Anteil fehlerhafter Einheiten) oder der Poissonverteilung (Anzahl Fehler pro Einheit). Unter bestimmten Voraussetzungen können beide Verteilungen der Einfachheit halber näherungsweise durch eine Normalverteilung ersetzt werden.

Für die Erstellung einer Regelkarte und Berechnung der Eingriffsgrenzen stehen folgende Optionen zur Verfügung:

 

 

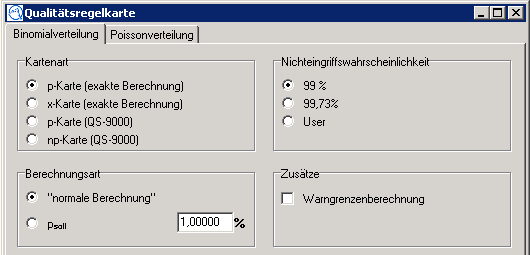
Nichteingriffswahrscheinlichkeit

 

Hier kann zwischen den vorgegebenen Nichteingriffswahrscheinlichkeiten 99% und 99,73% gewählt sowie unter "User" ein Wert selbst definiert werden. Bei Markierung des "User"-Feldes wird die Eingabe der gewünschten Nichteingriffswahrscheinlichkeit 1 - 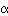 abgefragt.

 

Warngrenzenberechnung

Hier können Sie optional die Warngrenzenberechnung zuschalten. Die entsprechenden Werte werden dann im Menüunterpunkt "Nichteingriffswahrscheinlichkeit" zusätzlich angezeigt und entsprechend in die QRK eingezeichnet.

 

 

Kartenart - Binomialverteilung

 

p-Karte (exakte Berechnung)
Die p-Karte zeigt den Anteil fehlerhafter Einheiten einer untersuchten Menge. Der mittlere Anteil fehlerhafter Einheiten ist ein Schätzwert für den Anteil fehlerhafter Einheiten in der Grundgesamtheit.

x-Karte (exakte Berechnung)
Regelkarte für die Anzahl fehlerhafter Einheiten in einer Stichprobe. Als Schätzer für den Fehleranteil in der Grundgesamtheit dient der prozentuale Anteil fehlerhafter Einheiten. Ein konstanter Stichprobenumfang wird nicht vorausgesetzt.

p-Karte (QS-9000)
Sie ist identisch mit der p-Karte (exakte Berechnung) mit dem Unterschied, dass die Eingriffsgrenzen hier basierend auf dem Modell der Normalverteilung bestimmt werden.

np-Karte (QS-9000)
Bei der np-Karte wird die Anzahl fehlerhafter Einheiten einer Stichprobe gezählt. Sie ist vergleichbar mit der x-Karte, nur dass hier die Eingriffsgrenzen basierend auf der Normalverteilung berechnet werden und ein konstanter Stichprobenumfang vorausgesetzt wird.

 

Kartenart Poissonverteilung

 

u-Karte (exakte Berechnung)
Bei der u-Karte werden die Fehler pro Stichproben-Einheit gezählt. Der Stichprobenumfang sollte konstant sein. Die typische Anwendung hierfür ist die Fehlersammelkarte.

x-Karte (exakte Berechnung)
Regelkarte für die Anzahl der Fehler je Einheit.

u-Karte (QS-9000)
Sie ist identisch mit der u-Karte (exakte Berechnung) mit dem Unterschied, dass hier die Eingriffsgrenzen basierend auf dem Modell der Normalverteilung berechnet werden.

c-Karte (QS-9000)
Bei der c-Karte wird die Anzahl der Fehler in einer Stichprobe gezählt. Sie erfordert einen konstanten Stichprobenumfang oder eine konstante Menge Prüfmaterial. Die Eingriffsgrenzen errechnen sich basierend auf der Normalverteilung.