Modellbeurteilung

 

Die berechneten Ergebnisse sind:

•      Korrelationskoeffizient r: Je nachdem, ob Sie eine einfache Regression oder eine mehrfache Regression durchgeführt haben, steht an dieser Stelle der Wert des einfachen Korrelationskoeffizienten oder der Wert des multiplen Korrelationskoeffizienten (Erläuterung: siehe weiter unten).

•      Bestimmtheitsmaß R²: Wert, der den Anteil der durch das Modell erklärten Streuung von der insgesamt aufgetretenen Streuung der Zielgrößenwerte um den Zielgrößenmittelwert ausdrückt.

•      Korrigiertes Bestimmtheitsmaß R*²: Dieser Wert weist gegenüber dem Bestimmtheitsmaß R² die Besonderheit auf, dass der Wert davon beeinflusst wird, wie viele Parameter des Modells anhand der Stichprobendaten geschätzt werden müssen.

•      Restvarianz s²: Der Anteil der Streuung der Zielgrößenwerte, der nicht mehr durch das Modell erklärt wird.

•      Reststandardabweichung s: Positive Quadratwurzel der Restvarianz.

•      Ergebnis des Linearitätstests nach Fisher

•      Ergebnis des Tests auf Unabhängigkeit der Einflussgrößen

Einfacher Korrelationskoeffizient r

Das Ergebnis bei einer einfachen Regression ist der einfache Korrelationskoeffizient. Diese Kenngröße lässt sich als Maßzahl für die Stärke des linearen Zusammenhanges zwischen der Einfluss- und Zielgröße interpretieren. Der Wert liegt stets zwischen -1 und +1. Liegt der Wert in der Nähe von +1 oder -1, so ist dies ein erstes Indiz für eine starke lineare Beziehung zwischen beiden Variablen.

 

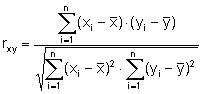
X = Merkmal, das als Einflussgröße betrachtet wird

Y = Merkmal, das als Zielgröße betrachtet wird

 

Multipler Korrelationskoeffizient r

Der multiple Korrelationskoeffizient ist eine Kenngröße zur Beschreibung des Grades der Übereinstimmung der Beobachtungsdaten der Zielgröße Y_i mit den vom Modell berechneten Schätzwerten für die Zielgröße Ŷ_i  . Der Wert des multiplen Korrelationskoeffizienten ist die positive Quadratwurzel des Bestimmtheitsmaßes R².

 

 

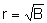
Bestimmtheitsmaß R²

Diese Kenngröße beschreibt, welcher Anteil der gesamten Streuung der Beobachtungswerte der Zielgröße von dem Regressionsmodell erklärt wird. Betrachtet man die nachfolgende Formel, so ist folgende Interpretation möglich: Über dem Bruchstrich steht die Summe der vom Modell erklärten quadrierten Abweichungen vom Mittelwert 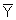 . Unterhalb des Bruchstriches befindet sich die Summe der quadrierten Abweichungen der Beobachtungswerte vom Mittelwert.

 

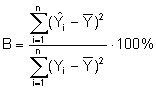
 Ŷ_i = Schätzwert für den i-ten Wert der Zielgröße (Ergebnis des Regressionsmodells)

Y_i= Tatsächlicher i-ter Beobachtungswert der Zielgröße

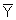= Mittelwert der Zielgrößenwerte

 

Allgemein gilt: Der Wert des Bestimmtheitsmaßes B ist positiv und kann zwischen 0 % und 100 % liegen. Befindet sich der Wert des Bestimmtheitsmaßes in dem Bereich zwischen 80% bis 100%, so ist dies ein erstes– aber leider nicht sicheres – Indiz für eine geeignete bis sehr gute Übereinstimmung zwischen dem Modell und den Daten.

Korrigiertes totales Bestimmtheitsmaß B’

Das korrigierte Bestimmtheitsmaß beinhaltet gegenüber dem Bestimmtheitsmaß B noch einen „Strafterm“, der berücksichtigt, wie viele Parameter des Modells anhand der zur Verfügung stehenden Werte geschätzt werden müssen. Der Sinn: Man kann mehrere Modelle mit einer unterschiedlichen Anzahl an Modellparametern miteinander vergleichen. Erweitert man z.B. ein lineares Modell um einen quadratischen Modellterm, so erhofft man sich eine bessere Anpassung. Ob diese tatsächlich gegeben ist oder nicht, wird anhand des Vergleiches der korrigierten Bestimmtheitsmaße beider Modelle entschieden. Ist der Wert des korrigierten Bestimmtheitsmaßes für das quadratische Modell genau so groß oder gar kleiner als beim linearen Modell, so spricht das für keine bessere Anpassung. Man kann also beim linearen Ansatz bleiben.

 

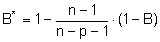
n = Anzahl der Wertepaare

p = Anzahl der zu schätzenden Modellparameter, inklusive der Konstanten.

B = Bestimmtheitsmaß

 

Restvarianz s²

Die Restvarianz ist der Anteil der Gesamtstreuung der Zielgrößenwerte, der nicht durch das Regressionsmodell erklärt werden kann.

 

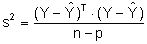
Y = Vektor der tatsächlich beobachteten Zielgrößenwerte

Ŷ = Vektor der aus dem Regressionsmodell geschätzten Zielgrößenwerte

n = Stichprobenumfang

p = Anzahl der geschätzten Koeffizienten, inklusive der Konstanten

 

Reststandardabweichung s

Positive Quadratwurzel der Restvarianz.

 

Ergebnisse des Linearitätstests nach Fisher (Lack-of-fit Test)

Dieser Test wird nur dann durchgeführt, wenn Beobachtungswerte aus Wiederholbedingungen vorliegen. Mit Wiederholbedingungen ist hier gemeint, dass mehr als ein Beobachtungswert der Zielgröße für eine ganz bestimmte Kombination der Einflussgrößenwerte vorliegt.

 

Wird die Nullhypothese verworfen, so ist der gewählte Modellansatz nicht konsistent mit den Beobachtungsdaten. In diesem Fall sollten der Modellansatz modifiziert werden.

 

Die Prüfgröße wird aus den quadrierten Abweichungen SS_Residual ermittelt, indem diese in zwei Anteile zerlegt wird: zum einen in den Anteil der Summe der quadrierten Abweichungen bezüglich der „reinen Zufallsabweichungen“ SS_{pure error} und zum anderen in den Anteil der Summe der quadrierten Abweichungen bezüglich des „Modellfehlers“ SSlack-of-fit.

 

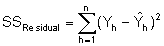
n = Stichprobenumfang

Y_h = h-ter Einzelwert der Zielgröße

Ŷ_h = h-ter Schätzwert der Zielgröße, berechnet aus dem Regressionsmodell

 

 

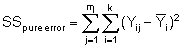
m_i = Anzahl der „Wiederholwerte“ der Zielgröße bei der i-ten Einstellkombination der Einflussgrößen

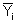Y_ij = Der j-te Einzelwert der mi Zielgrößenwerte bei der i-ten Einstellkombination der Einflussgrößen

= Mittelwert der m_i Zielgrößenwerte bei der i-ten Einstellkombination der Einflussgrößen

 

 

 

 

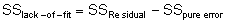
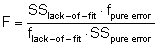
f_{pure error} = Freiheitsgrade für die “reine Zufallsstreuung”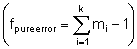  

f_lack-of-fit = Freiheitsgrade für die Modellabweichungen (f_Redisual – f_{pure error}, mit f_Residual = n-p)

F = Prüfgröße des Lack-of-fit Tests

 

Die Prüfgröße F wird mit den kritischen Werten der F-Verteilung für f1 = fl_ack-of-fit und f2 = f_{pure error} verglichen. Die kritischen Werte werden für die Signifikanzniveaus a = 5%, a = 1% und a = 0,1 % berechnet.

 

Test auf Unabhängigkeit von allen Einflussgrößen

Dieser Test prüft simultan, ob die Zielgröße unabhängig von sämtlichen Einflussgrößen ist, die im Regressionsansatz berücksichtigt worden sind. Wird die Nullhypothese nicht verworfen, so ist zu überlegen, ob die richtigen Einflussgrößen ausgewählt worden sind bzw. ob ein anderer Modellansatz sinnvoll ist.

Prüfgröße:  

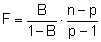
B = Bestimmtheitsmaß

n = Stichprobenumfang

p = Anzahl Koeffizienten, inklusive der Konstanten

 

Die kritischen Werte sind die Quantile 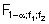 einer F-Verteilung mit den Freiheitsgraden f1 = p-1und f2 = n-p für die Vertrauensniveaus 1-a = 95%, 1-a = 99 % und 1-a = 99,9 %.