Koeffizienten

Polynome (nur bei quasilinearer Regression sichtbar)

Das Auswahlfeld Polynome ist für das Hinzufügen von Koeffizienten für quadratische, kubische und weitere Effekte höheren Grades gedacht. Diese Funktionalität steht allerdings nur bei der einfachen und mehrfachen quasilinearen Regression zur Verfügung.

Um Koeffizienten für die Effekte höheren Grades in das Modell aufzunehmen, aktivieren Sie die zugehörigen Checkboxen mit der Maus. Durch einen weiteren Mausklick wird die Checkbox wieder deaktiviert und der zugehörige Koeffizient aus dem Modell entfernt. Das Modell kann auch manuell angepasst werden. Klicken Sie dazu auf die Schaltfläche manuelle Auswahl (Beschreibung folgt weiter unten).

Normierung

Dieses Auswahlfeld steht zur Verfügung, wenn Grenzwerte für die lineare Transformation (Fenster Daten) eingegeben worden sind.

Wählt man entsprechend Eingabe, so erfolgt die lineare Transformation derart, dass der kleinste Merkmalswert dem unteren eingegeben Grenzwert E_un und der größte Merkmalswert dem oberen eingegebenen Grenzwert E_ob entspricht.

Bei der Normierung auf min./max. Werte entspricht der kleinste Merkmalswert dem unteren Grenzwert E_un = -1 und der größte Merkmalswert dem oberen Grenzwert E_ob = +1.

Schrittweiser Abbau (t-Test)

Diese Funktionalität ist nur bei der mehrfachen Regression verfügbar. Mit dem schrittweisen Abbau werden nicht signifikante Modellterme aus dem Modell entfernt.

Das Abbau-Prinzip in Kürze:

Zunächst wird vom Rechner das Regressionsmodell mit allen Koeffizienten – gemäß dem gewählten Ansatz - berechnet. Für jeden Koeffizienten wird eine Prüfgröße t berechnet und ein t-Test auf Signifikanz durchgeführt (Beschreibung der Prüfgröße siehe weiter unten unter Ergebnistabelle). Von allen Koeffizienten, die als nicht signifikant eingestuft wurden, wird der Koeffizient mit dem kleinsten t-Wert ausgewählt und aus dem Modellansatz entfernt. Danach wird das Modell erneut berechnet und das Verfahren wiederholt. Der schrittweise Abbau wird üblicher Weise so lange fortgesetzt, bis nur noch signifikante Koeffizienten übrig sind.

Es gibt zwei Varianten des schrittweisen Abbaus: eine manuelle und eine automatisierte Durchführung des Verfahrens.

Manuelle Durchführung des schrittweisen Abbaus

Die erste Variante funktioniert buchstäblich schrittweise: Mit jedem Mausklick auf das Icon $S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image61.gif$ wird jeweils genau ein einziger Modellterm entfernt (sofern dieser nicht signifikant ist).

Automatisierte Durchführung des schrittweisen Abbaus

Geben Sie zunächst das gewünschte Vertrauensniveau für den t-Test ein. Anschließend vollziehen Sie einen Mausklick auf dem Icon $S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image62.gif$ . Dadurch wird der schrittweise Abbau solange durchgeführt, bis nur noch signifikante Koeffizienten übrig sind. Das heißt, Sie erhalten sofort das Endergebnis ohne die Zwischenergebnisse.

Mit einem Mausklick auf das Icon $S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image63.gif$ wird der schrittweise Abbau – stets vollständig - rückgängig gemacht.

Manuelle Auswahl

Möchten Sie die Koeffizientenauswahl ihres Modells manuell anpassen, so klicken Sie auf die Schaltfläche. Daraufhin erscheint das Fenster Auswahl bearbeiten. In diesem Fenster können Sie manuell die Modellkoeffizienten an- und abschalten, indem Sie mit der Maus auf die entsprechenden Felder in der Spalte Auswahl klicken.

Koeffizienten

Das Fenster enthält mehrere Berechnungsergebnisse, die in Spalten angeordnet sind. In der Überschrift befindet sich der berechnete Wert des Korrelationskoeffizienten r und der Wert des Bestimmtheitsmaßes B. Darunter befinden sich, nach Spalten geordnet, folgende Angaben.

• Merkm.: Die vom Benutzer vergebene Merkmalsnummer.

• Merkm. Bez.: Die Bezeichnung des Merkmals.

• x_i : Der Typ des geschätzten Koeffizienten, wie z.B. Konstante, Wechselwirkung, etc.

• b_i : Die aus der Stichprobe berechneten Schätzwerte für die Koeffizienten

• b_i : Der zweiseitige 95%-Vertrauensbereich des geschätzten Modellkoeffizienten

• s_ci : Die Standardabweichung des geschätzten Koeffizienten

• |t_i| : Der Betrag der Prüfgröße t des durchgeführten t-Tests für den Koeffizienten

• |t_i| : Die Balkengrafik des Testergebnisses des t-Tests für den Koeffizienten

(H₀: Der Wert des Koeffizient der Grundgesamtheit ist 0 versus

H₁: Der Wert des Koeffizienten der Grundgesamtheit ist ungleich 0)

• VIF: Der Wert des Varianzeninflationsfaktors des Merkmals

Schätzwerte für die Koeffizienten bi

Die aus der Stichprobe berechneten Werte b_i der Koeffizienten des Regressionsmodells sind Schätzwerte für die „wahren“ Koeffizienten ß_i des Modells der Grundgesamtheit. Die folgende Formel stellt in Matrix-Schreibweise die Berechnung der Schätzwerte des linearen Modells dar.

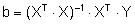
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image55.gif$

b = Vektor der Modellkoeffizienten

X = Matrix der Einflussgrößen

Y = Vektor der Beobachtungswerte der Zielgröße

Individuelle zweiseitige 95%-Vertrauensbereiche für die Koeffizienten bi

Dargestellt sind die Zahlenwerte des zweiseitigen 95%-Vertrauensbereiches für jeden einzelnen Koeffizienten ß_i. Rechnerisch erhält man für den i-ten Koeffizient b_i die untere Vertrauensbereichsgrenze b_un und die obere Vertrauensbereichsgrenze b_ob wie folgt:

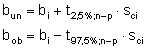
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image56.gif$

b_i= Schätzwert des i-ten Koeffizienten aus der Stichprobe

s_ci = Standardabweichung des i-ten Koeffizienten

n = Stichprobenumfang

p = Anzahl geschätzter Koeffizienten, inklusive der Konstanten

t = Quantil der t-Verteilung mit f = n-p Freiheitsgraden

Standardabweichung sci des geschätzten Koeffizienten

Die Standardabweichungen der geschätzten Koeffizienten erhält man aus der Varianz-Kovarianz-Matrix Var(b), die hier in Matrix-Schreibweise dargestellt ist:

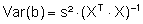
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image57.gif$

s² = Restvarianz, also der Anteil der Gesamtstreuung der Zielgrößenwerte, der nicht durch das Regressionsmodell erklärt werden kann.

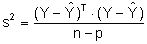
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image58.gif$

Y = Vektor der tatsächlich beobachteten Zielgrößenwerte

Ŷ = Vektor der aus dem Regressionsmodell geschätzten Zielgrößenwerte

n = Stichprobenumfang

p = Anzahl der geschätzten Koeffizienten, inklusive der Konstanten

Die Diagonalelemente der Varianz-Kovarianz-Matrix Var(b) sind die Varianzen der Koeffizienten. Die positive Quadratwurzel dieser Diagonalelemente entspricht den Standardabweichungen der Koeffizienten, deren Werte in der Ergebnismaske dargestellt sind.

Betrag der Prüfgröße t für den t-Test

Die wahren Koeffizienten könnten auch den Wert ß_i = 0 haben. Um dies zu prüfen, wird ein t-Test durchgeführt (siehe nächster Abschnitt). Der Betrag der Prüfgröße t_i ergibt sich nach folgender Beziehung:

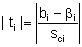
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image60.gif$

b_i = Schätzwert des i-ten Koeffizienten aus der Stichprobe

ß_i = Vorgabewert für den i-ten Wert des Koeffizienten der Grundgesamtheit (hier: ß_i = 0)

s_ci = Standardabweichung des i-ten Koeffizienten

Balkengrafik des Testergebnisses von dem t-Test

Auf der Basis der zuvor errechneten Prüfgröße wird der t-Test durchgeführt. Basis für den Test ist die nachfolgend dargestellte Kombination aus Null- und Alternativhypothese.

H0: ß_i= 0 versus H1: ß_i≠ 0.

In der Balkengrafik sind drei rot eingefärbte, senkrechte Linien zu sehen. Diese repräsentieren die Schwellenwerte der t-Verteilung für die Signifikanzniveaus – von links nach rechts gelesen - α = 5%, α = 1% und α = 0,1%. Überschreitet die Prüfgröße die Schwellenwertlinie für das Signifikanzniveau α = 5%, so erhält der Prüfgrößenwert ein Sternchen (*). Wird die Schwellenwertlinie für α = 1 % überschritten, so erhält der Prüfgrößenwert zwei Sternchen (**). Bei Überschreitung der dritten Schwellenwertlinie für α = 0,1 % erhält die Prüfgröße drei Sternchen (***). Bleibt der Balken unterhalb der Schwellenwertlinien, so ist das Testergebnis als nicht signifikant eingestuft und der Prüfgrößenwert erhält kein Sternchen.

Varianzeninflationsfaktor VIF

Diese Spalte ist nur bei der mehrfachen Regression sichtbar. Der VIF-Wert gibt Ihnen ein Indiz, ob das Merkmal mit einem anderen Merkmal stark korreliert. Der Idealwert ist VIF=1, was bedeutet, dass keine Korrelation vorliegt. Je größer der Wert ist, umso stärker ist die Korrelation mit anderen Merkmalen. Der Name leitet sich aus dem Gedanken ab, wie stark die Streuung des betrachteten Merkmals durch die Korrelation mit den anderen Merkmalen aufgebläht wird. Ist VIF > 10, so liegen starke Abhängigkeiten zwischen dem betrachteten Merkmal und einem oder mehreren anderen Merkmalen vor. Wird das Modell für Prognosen verwendet, so sollte man sehr vorsichtig bei Extrapolationen sein.

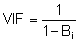
$S:\DEVEL_AD\HELP\HELP_ME8\QDASGER\!SSL!\Printed_Documentation\!doc_tmp_folder_1\image64.gif$

B_i = Merkmalsbezogen berechnetes Bestimmtheitsmaß (auch Quadrat des multiplen Korrelationskoeffizienten genannt). Der Wert des multiplen Korrelationskoeffizienten drückt die Abhängigkeit des betrachteten Merkmals von allen übrigen Merkmalen aus.