Erklärung der Teststatistik am Beispiel aus dem VDA 5

 

Die Ergebnisse der Wiederholungsprüfungen an den 40 Prüfobjekten wurden in die dazugehörige Matrix eingetragen. Anschließend wird überprüft, ob es signifikante Unterschiede zwischen den Häufigkeiten links und rechts der Hauptdiagonale gibt. Dazu werden die Häufigkeiten von

 

•     Prüfer A Klasse 2 (n_2;1)mit Prüfer B Klasse 2 (n_1;2)

•     Prüfer A Klasse 3 (n_3;1)mit Prüfer B Klasse 2 (n_1;3)

•     Prüfer A Klasse 3 (n_3;2)mit Prüfer B Klasse 2 (n_2;3)

 

miteinander verglichen.

 

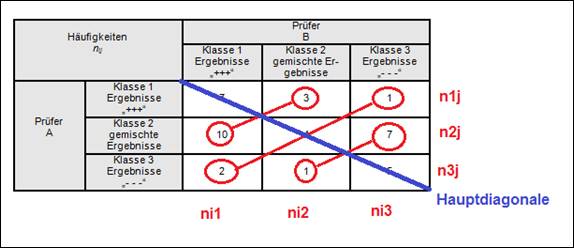
Anmerkung: Bei den Häufigkeiten n_i/n_j entspricht i der Zeile und j der Spalte der Matrix

 

Dazu wird ein Chi² Test durchgeführt.

 

 

 

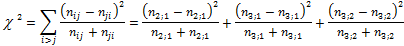
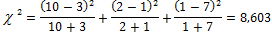
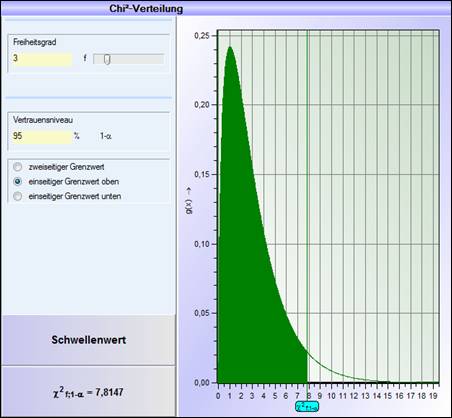
Das Ergebnis der Teststatistik wird mit dem kritischen Wert von 7,815 verglichen. Der kritische Wert entspricht dem Schwellenwert des einseitigen oberen Grenzwertes einer Chi² Verteilung mit dem Freiheitsgrad von 3 und einem Vertrauensniveau von 95%. Ist die Teststatistik kleiner als der kritische Wert, so liegt der Wert innerhalb des 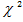Quantils von 95% (grüner Bereich der unteren Grafik).

 

Da im Beispiel die Teststatistik mit 8,603 über den kritischen Wert liegt, wird die ursprüngliche Nullhypothese H0: „Beide Prüfer ermitteln vergleichbare Ergebnisse“ mit einer Irrtumswahrscheinlichkeit vo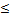n  5% abgelehnt (verworfen) und die Alternativhypothese H1: „Beide Prüfer ermitteln unterschiedliche Ergebnisse“ angenommen.