Studentisierte Residuen
Grafiken der studentisierten Residuen
Mit Hilfe der Residuen-Grafiken soll eine visuelle Bewertung des Modells vorgenommen werden.
Folgende Grafiken werden angezeigt:
1. Studentisierte Residuen-Werteverlauf in Beobachtungsreihenfolge
2. Studentisierte Residuen im Wahrscheinlichkeitsnetz der Normalverteilung
3. Studentisierte Residuen über die geschätzten Zielgrößenwerte
Werteverlauf der studentisierte Residuen
Diese Grafik dient der Beurteilung des Verhaltens der Werte über die Zeit. Ein idealer Werteverlauf der Residuen zeigt ein Zufallsmuster. Das heißt, es sollten keine systematischen Verlaufsmuster zu sehen sein, wie z.B.
• Trendverläufe
• u- oder n-förmige Verläufe
Wahrscheinlichkeitsnetz der studentisierte Residuen
Das Regressionsmodell sollte die Streuung der Zielgröße möglichst vollständig erklären. Den Anteil der gesamten Streuung, den das Modell nicht erklären kann, sollte eine „zufällige Reststreuung“ sein. Zeigen die studentisierten Residuen im Wahrscheinlichkeitsnetz nahezu den Verlauf einer Geraden, so ist das ein Indiz dafür, dass die verbliebene Reststreuung tatsächlich eine Zufallsstreuung ist.
Studentisierte Residuen in Abhängigkeit von den Schätzwerten
In dieser Grafik sind die studentisierten Residuen über die aus dem Modell berechneten Werte der Zielgröße (=fitted Values) dargestellt. Ein Indiz für die Übereinstimmung von dem Modell mit den Beobachtungswerten ist gegeben, wenn
• das Residuen-Streumuster einen horizontalen Verlauf zeigt.
• die Streubreite der Residuen im gesamten Bereich der Zielgröße gleich breit ist.
Berechnung der studentisierten Residuen
Differenz zwischen den beobachteten Zielgrößenwerten und den aus dem Modell berechneten Zielgrößenwerten, dividiert durch die geschätzte Standardabweichung der Residuen.
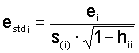
ei = Residuum
s(i) = Die Reststandardabweichung, wenn man die i-te Zeile bei der Modellberechnung nicht berücksichtigt.
hii = i-tes Diagonalelement der Hat-Matrix H, mit H =X×(XT·X)-1·XT.