Studentisierte Residuen

 

Grafiken der studentisierten Residuen

Das Fenster besteht aus drei Grafiken

1. Studentisierte Residuen-Werteverlauf in Beobachtungsreihenfolge

2. Studentisierte Residuen im Wahrscheinlichkeitsnetz der Normalverteilung

3. Studentisierte Residuen über die geschätzten Zielgrößenwerte (engl. fitted values)

 

Werteverlauf der studentisierten Residuen

Diese Grafik dient der Beurteilung des Verhaltens der Werte über die Zeit. Hat es Störungen gegeben? Gibt es Unstimmigkeiten im zeitlichen Verlauf? Liegen einzelne Werte ungewöhnlich weit entfernt von den übrigen Werten?

 

Ein idealer Werteverlauf der studentisierten Residuen zeigt ein Zufallsmuster. Das heißt, es sollten keine systematischen Verlaufsmuster zu sehen sein, wie z.B.

•      Trendverläufe

•      u- oder n-formige Verläufe

 

Wahrscheinlichkeitsnetz der studentisierten Residuen

Die studentisierten Residuen sollten nahezu den Verlauf einer Geraden bilden. Hinweis: Eigentlich streuen die studentisierten Residuen – wie der Name schon sagt – t-verteilt. Das heißt, bei kleinen Stichprobenumfängen sind leichte Abweichungen von dem Verlauf einer Geraden zu erwarten; aufgrund der Tatsache, dass t-verteilte Größen bei kleinen Stichprobenumfängen vergleichsweise breiter streuen als normalverteilte Größen.

 

Studentisierte Residuen in Abhängigkeit von den Schätzwerten

In dieser Grafik sind die Residuen über die aus dem Modell berechneten Werte der Zielgröße (=fitted Values) dargestellt. Ein Indiz für die Übereinstimmung von dem Modell mit den Beobachtungswerten ist gegeben, wenn

•      das Residuen-Streumuster einen horizontalen Verlauf zeigt.

•      die Streubreite der Residuen im gesamten Bereich der Zielgröße gleich breit ist.

 

Studentisierte Residuen s_std

Differenz zwischen den beobachteten Zielgrößenwerten und den aus dem Modell berechneten Zielgrößenwerten (engl. fitted values), dividiert durch die geschätzte Standardabweichung der Residuen.

 

 

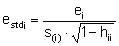
e_i = Residuum

s_(i) = Die Reststandardabweichung, wenn man die i-te Zeile bei der Modellberechnung nicht berücksichtigt.

h_ii = i-tes Diagonalelement der Hat-Matrix H, mit H =X·(X^T·X)^-1·X^T.