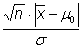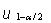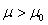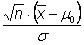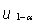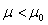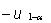Einstichproben u-Test
*** Diese Seite ist in Bearbeitung ***
Trotz aller Bemühungen lassen sich Fehler in der Beschreibung nie vollständig vermeiden. Für Ihre Hinweise und Anregungen sind wir jederzeit dankbar (Hotline: hotline@q-das.de, +49 (6201) 3941-14).
Einstichproben u-Test
Vergleich des Erwartungswertes einer Normalverteilung mit einem vorgegebenen Wert.
Standardabweichung σ ist bekannt.
|
Nullhypothese H0 |
Alternativhypothese H1 | |||
|
Der Erwartungswert der Grundgesamtheit ist gleich dem vorgegebenen Wert µ0
|
Der Erwartungswert der Grundgesamtheit ist nicht gleich dem vorgegebenen Wert µ0
| |||
|
|
| |||
|
|
| |||
|
Alternativhypothese |
Die Nullhypothese | |||
|
|
Prüfgröße |
|
kritischer Wert | |
|
zweiseitig |
|
> |
| |
|
einseitig |
|
> |
| |
|
einseitig |
|
< |
| |
|
|
|
|
|
|
Mehrstichproben Lage-Test
*** Diese Seite ist in Bearbeitung ***
Trotz aller Bemühungen lassen sich Fehler in der Beschreibung nie vollständig vermeiden. Für Ihre Hinweise und Anregungen sind wir jederzeit dankbar (Hotline: hotline@q-das.de, +49 (6201) 3941-14).
Test von Kruskal und Wallis XE "Kruskal und Wallis"
Der Kruskal-Wallis-Test prüft ohne eine Normalverteilung vorauszusetzen (lediglich eine stetige Verteilung wird gefordert), ob die Mittelwerte von p Messreihen der Längen n1, ..., np als signifikant verschieden angesehen werden können.
Dabei geht man so vor, dass man zunächst den N Messwerten Y11, ..., Ypnp Rangzahlen rij zuordnet, wobei der r-kleinste Messwert Yij den Rang rij = r erhält. Beim Vorliegen von Bindungen, d.h. wenn mehrere Messwerte gleich sind, werden jeweils die mittleren der in Frage stehenden Ränge zugewiesen, vgl. Beispiel. Präziser formuliert:
Treten insgesamt g verschiedene Messwerte z1 < z2 < ... < zg auf
und zwar zk genau tk-mal, tk 1, 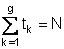 ,
,
so entspricht der Fall g < N [also tk > 1 für mindestens ein k] gerade dem Vorliegen von Bindungen.
Dem Messwert Yij wird jeweils der Rang 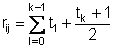 zugeordnet.
zugeordnet.
Falls Yij = zk ist; dabei wird to = 0 gesetzt.
Für jede der Messreihen berechnet man dann die Summe der Ränge, die den Messwerten der betreffenden Reihe zugeordnet sind:
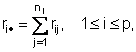
und hieraus die Prüfgröße
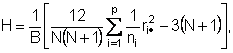
wobei 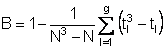
eine Korrekturgröße ist, die in Abwesenheit von Bindungen
gerade den Wert B=1 annimmt. Es kann jedoch auch beim Vorliegen von „wenigen“
Bindungen, etwa wenn die Anzahl der verschiedenen Messwerte 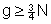 ist, immer noch B=1 gesetzt werden.
ist, immer noch B=1 gesetzt werden.
Zum vorgegebenen Niveau , 0 < < 1, wird nun auf signifikante Unterschiede in den Reihenmitteln geschlossen, wenn gilt
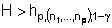
Die kritischen Werte sind unter anderem in [3] angegeben.
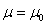 (zweiseitig)
(zweiseitig)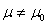 (zweiseitig)
(zweiseitig)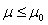 (einseitig)
(einseitig)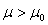 (einseitig)
(einseitig)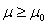 (einseitig)
(einseitig)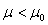 (einseitig)
(einseitig)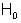 wird zugunsten
der
wird zugunsten
der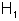 verworfen, falls
verworfen, falls