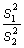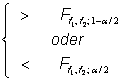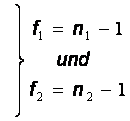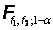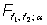Zweistichproben F-Test
*** Diese Seite ist in Bearbeitung ***
Trotz aller Bemühungen lassen sich Fehler in der Beschreibung nie vollständig vermeiden. Für Ihre Hinweise und Anregungen sind wir jederzeit dankbar (Hotline: hotline@q-das.de, +49 (6201) 3941-14).
Zweistichproben F-Test
Vergleich der Varianzen von zwei Normalverteilungen.
|
Nullhypothese H0 |
Alternativhypothese H1 | ||||
|
Die Varianzen der Grundgesamtheiten sind gleich
|
Die Varianzen der Grundgesamtheiten sind nicht gleich
| ||||
|
|
| ||||
|
|
| ||||
|
Alternativhypothese |
Die Nullhypothese | ||||
|
|
Prüfgröße |
kritischer Wert | |||
|
zweiseitig |
|
|
| ||
|
einseitig |
|
> |
| ||
|
einseitig |
|
< |
| ||
|
|
|
|
|
|
|
Zweistichproben F-Test
Vergleich der Varianzen von zwei Normalverteilungen
Beispiel aus Six Sigma Lehrgang: Drehen von Distanzhülsen
33,1±0,15

Problemstellung:
Auf zwei baugleichen Drehmaschinen werden Distanzhülsen gedreht. Das kritische Merkmal ist die Länge der Distanzhülsen. Die Distanzhülsen beider Maschinen werden zu einem Fertigungslos zusammengefasst. Man hat festgestellt, dass die Streuung der Längen im Fertigungslos zu groß ist, um prozessfähig zu sein. Es soll nun geprüft werden, ob beide Maschinen gleich produzieren, oder ob es Unterschiede zwischen den beiden Drehmaschinen bezüglich ihrer Streuung gibt, die nicht mit einer zufälligen Abweichung erklärt werden kann.
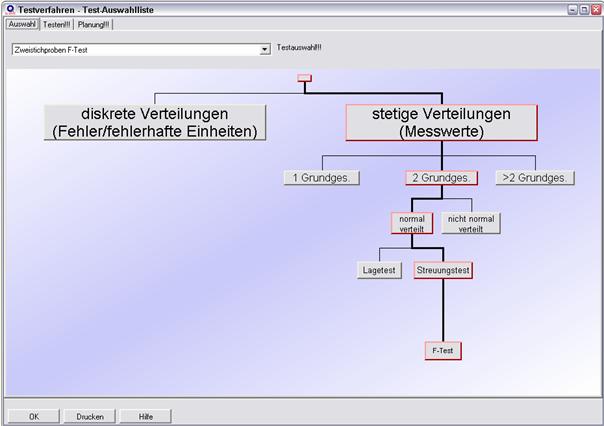
Planung:
Erforderliche Eingaben:
1. Welche Differenz zwischen den
Standardabweichungen
wird – aus sachlicher Sicht – als kritisch
angesehen?
a. Man verwendet das Verhältnis λ = σ1/σ2 für die Planung
b. Wenn eine der beiden Standardabweichung s1 und s2 den doppelten Wert der anderen Standardabweichung hat, so soll das erkannt werden können
c. Gewählt: λ = 2
2. Welche Irrtumswahrscheinlichkeit (Fehler erster Art α) soll akzeptiert werden?
a. Gewählt: α = 5 %
3. Welcher Fehler zweiter Art (β) soll akzeptiert werden?
a. Gewählt: β = 10 %
4. Da unbekannt ist, ob ein Unterschied zwischen beiden Maschinen besteht, soll zweiseitig getestet werden
a. Gewählt: Zweiseitige Fragestellung
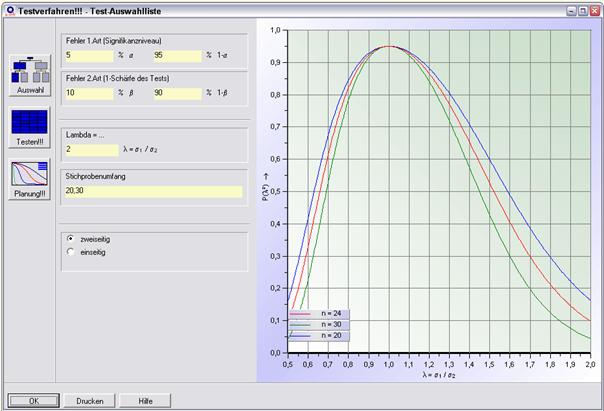
Das Ergebnis der Testplanung ergibt einen Mindeststichprobenumfang von n = 24 zu prüfenden Teilen (pro CNC-Maschine).
Testdurchführung:
Benötigte Kennwerte bzw. Parameter pro Stichprobe:
• Stichprobenumfang (aus Planung ergibt sich n=24)
• Standardabweichung bzw. Varianz
Datei mit qs-STAT Daten: CNC-F_TEST.DFQ
Die Datei besteht aus den beiden Merkmalen, die je 24 gemessene Werte der CNC Maschine 1 bzw. 2 enthalten.
Die Kennwerte der beiden Stichproben können durch Ziehen des jeweiligen Merkmals aus der Merkmalsliste auf den Eingabebereich übernommen werden (vgl. Kapitel 1.4).
Der Test wird zweiseitig durchgeführt (vgl. Planung)
Die Testdurchführung mit ok anstoßen.
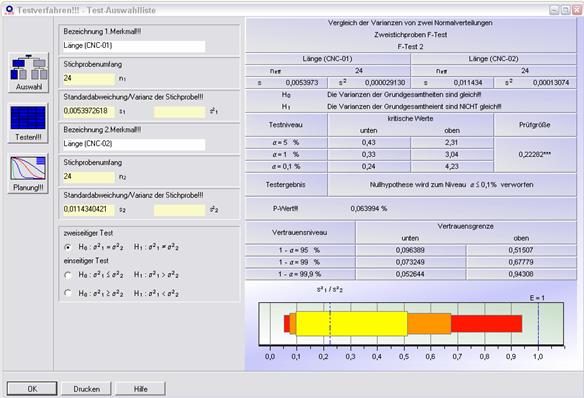
Ergebnis:
Die Nullhypothese wird verworfen, das heißt, die Varianzen der Grundgesamtheiten sind nicht gleich und die Stichprobe von der 2. CNC-Maschine streut (hoch-)signifikant stärker, als die Stichprobe, die der ersten Maschine entnommen wurde.
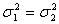 (zweiseitig)
(zweiseitig)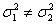 (zweiseitig)
(zweiseitig)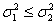 (einseitig)
(einseitig)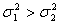 (einseitig)
(einseitig)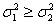 (einseitig)
(einseitig)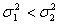 (einseitig)
(einseitig)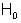 wird zugunsten
der
wird zugunsten
der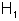 verworfen, falls
verworfen, falls