Definitionen und Grundlagen der Berechnung

 

*** Trotz aller Bemühungen lassen sich Fehler in der Beschreibung nie vollständig vermeiden. Für Ihre Hinweise und Anregungen sind wir jeder­zeit dankbar (Hotline: hotline@q-das.de, +49 (6201) 3941-14). ***

 

 

 

Als Maß für die PAA dient die Risikokennzahl R_k eines Teiletyps. Diese ergibt sich als Summe der Risikokennzahlen aller Merkmale des Teiletyps, die bei dem untersuchten Teil Anomalien aufweisen.

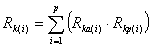        p=Anzahl der für ein Teil i gefundenen Anomalien

 

Bestimmung der Anomalien für den offline Modus:

 

Zur Bestimmung der Anomalie wird ein Parameter lambda_i berechnet:

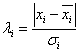
Dabei sind x_i und sigma_i der lokale Mittelwert bzw. die lokale Standardabweichung aus den unmittelbar zum Wert i benachbarten Teilen. Mittelwert und Standardabweichung werden aus n_lokal Werten berechnet. Die Anzahl (n_lokal) ist entweder fest vorgegeben oder wird aus folgender Formel berechnet:

 

 

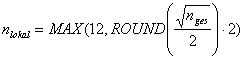                ROUND: auf-/ abrunden auf ganze Zahl

n_lokal ist immer eine gerade Zahl (>= 12).

Daher müssen Messwerte von mindestens 13 Teilen (12 + das zu untersuchende) vorliegen, um eine PAA durchführen zu können.

 

Für diese Anzahl (n_lokal) Teile werden der lokale Mittelwert und die lokale Standardabweichung berechnet. Dabei ist zu beachten, dass der Wert des zu beurteilenden Teiles (Laufindex i) in die Berechnung nicht einfließt und daher in den Formeln jeweils wieder von der Summe subtrahiert wird.

 

Bei den ersten n_lokal / 2 Teilen können der Mittelwert und die Standardabweichung noch nicht symmetrisch berechnet werden. Daher gilt für die ersten zu testenden Teile (z.B. Bandanlauf; für n_lokal = 12 kann erst ab dem 7. Teil eine symmetrische Betrachtung erfolgen):

 

Lokaler Mittelwert 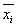 für :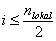

 

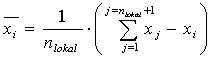
Lokale Standardabweichung :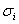

 

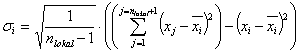
Im kontinuierlichen (symmetrischen) Testbetrieb gilt:

 

Lokaler Mittelwert 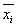 für :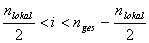

 

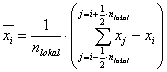
Lokale Standardabweichung :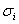

 

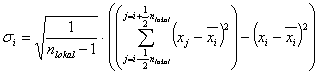
Für die letzten Teile (z.B. Bandabschaltung) gilt:

Lokaler Mittelwert 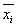 für :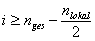

 

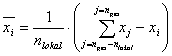
Lokale Standardabweichung :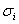

 

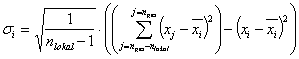
Ergibt sich ein lambda_i >= 6, wurde eine Anomalie bei dem i-ten gemessenen Teil gefunden.

 

Die Signifikanz der Anomalie (R_ka) ergibt sich dann aus einer Zuordnungsvorschrift, wie sie folgende Grafik zeigt:

 

Abbildung 1 Definition R_ka

 

Die Signifikanz des Parameters (R_kp) in Abhängigkeit von der Merkmalsklasse wird ebenfalls tabellarisch definiert.

 

Abbildung 2 Definition R_kp

 

Aus R_ka und R_kp wird die Risikokennzahl für die Anomalie eines Merkmals an der Stelle i berechnet:

          R_k(i) = R_kp(i) * R_ka(i)

Im online Modus werden immer die n_lokal vorhergehenden Werte berücksichtigt. Daher gilt:

Lokaler Mittelwert 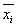 für :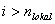

 

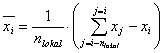
Lokale Standardabweichung :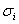

 

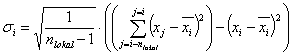
Die Risikokennzahl wird wie im offline Modus berechnet.