Best-Fit-Move – Mittelwert / Letzter Wert

 

Diese Funktion findet Anwendung bei Positionstoleranzen, wie sie z.B. für Bohrungen benötigt werden. Bei Bohrungen ist die zulässige Abweichung von der Solllage durch einen Toleranzkreis bzw. durch eine Toleranzellipse festgelegt. Eine eventuell erforderliche Lagekorrektur einer einzelnen Bohrung ist verhältnismäßig einfach zu realisieren. Was aber, wenn die Lage von mehreren Bohrungen zugleich betrachtet werden muss?

Häufig werden mehrere Bohrungen an einer Maschine auf einmal gefertigt, so z.B. bei Motorblöcken. Ist nun die Lage von den Bohrungen nicht befriedigend, so stellt sich die Frage nach einer Lage-Korrektur. Vor dem Hintergrund, dass das Einrichten der Werkzeuge verhältnismäßig aufwendig ist, sucht man nach einem „schnellen“ Weg für die Lagekorrektur, ohne die Werkzeuge erneut einrichten zu müssen.

Vorschlag für eine „einfache“ Lagekorrektur

Das Verfahren des „Best fit move“ ist ggf. eine Möglichkeit zur Lösung des Problems:
Die Bohrungen eines Motorblocks werden zu einer gemeinsamen Gruppe zusammengefasst. Es werden mehrere gefertigte Blöcke vermessen. Die Daten werden in qs-STAT® eingegeben, zu einer Gruppe zusammengefasst und mit dem Verfahren „Best fit move“ ausgewertet. Dabei wird von dem Programm mit einem Ausgleichsalgorithmus die Lagekorrektur des gesamten Motorblocks errechnet. Das Programm gibt Korrekturwerte für beide Achsrichtungen aus und einen Korrekturwinkel. Die Lage der zu bearbeitenden Werkstücke wird an der Bearbeitungsmaschine entsprechend den Korrekturwerten neu eingestellt. Dadurch ergibt sich eine Verbesserung der Lage von dem gesamten Bohrlochmuster. D.h., die Differenzen zwischen den Ist- und Sollpositionen sind dann kleiner.

Freie Wahl des Bezugssystems

Das Programm kann die Korrekturwerte für die folgenden Bezugssysteme berechnen:

1. Bezug für die Korrekturwertberechnung ist der Schwerpunkt des Bohrlochmusters

2. Bezug für die Korrekturwertberechnung ist der Koordinatenursprung

In der nachfolgenden Abbildung sieht man ein Beispiel für die Drehung um den Koordinatenursprung der Maschine. Das kleine Sternchen links im Bild ist der Koordinatenursprung, der als Bezugspunkt für den Drehwinkel verwendet wird. Die Korrekturwerte sind damit nur für das gewählte Bezugssystem gültig.

 

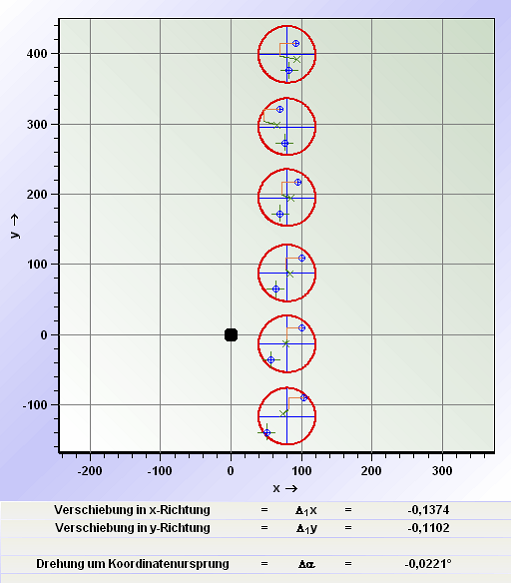
Die numerische Ausgabe der Korrekturwerte ist im Fußteil der Abbildung enthalten. Wie man aus den Textfeldern schon vermuten kann, bietet das Programm zwei Berechnungsverfahren zur Bestimmung der Korrekturwerte an:

Berechnungsverfahren 1

Hier wird erst die Korrektur für die Verschiebung in den Koordinatenachsen berechnet und anschließend der Korrekturwert für den Winkel.

Berechnungsverfahren 2

Es wird erst der Korrekturwert für den Drehwinkel und anschließend die Korrekturwerte für die Verschiebung in den Koordinatenachsen berechnet.

 

Die Einstellungen können mit dem Button „Spezial“ angepasst werden. Standardmäßig werden die Einstellungen der Strategie verwendet, mit der Option „Untere Einstellung … verwenden“ können eigene Angaben gemacht werden.

 

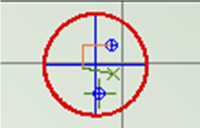
Das nächste Bild stellt einen Ausschnitt aus der Zeichnung vergrößert dar.

Das obere Kreuz stellt die ursprüngliche Lage des Mittelwertes von den Messwerten dar. Das zweite Kreuz stellt die berechnete Lage des Mittelwertes nach der Korrektur dar. Der Weg der Verschiebung ist eingezeichnet. Der braun eingezeichnete Weg ist die Korrektur des Winkels. Die blau und rot eingezeichneten Geraden sind die Korrekturverschiebungen in x- und y-Richtung.